Recognizable language

In mathematics and computer science, a recognizable language is a formal language that is recognized by a finite state machine. Equivalently, a recognizable language is one for which the family of quotients for the syntactic relation is finite.

Definition

Given a monoid M, a language over M is simply a subset 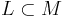$L\subset M$ . Such a language is said to be recognizable over M if there is a finite state machine over M that accepts L as an input. A finite state machine over M is simply one that takes elements of M as input, and accepts or does not accept them.

The family of recognizable languages over M is commonly denoted as 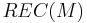$REC(M)$ .

Examples

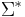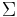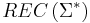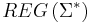If M is the free monoid $\Sigma^*$ over some alphabet $\Sigma$ , then the family $REC\left(\Sigma^*\right)$ is just the family of regular languages $REG\left(\Sigma^*\right)$ .